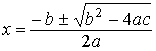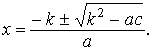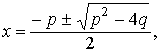2.1.2. Квадратные уравнения.

Теория и примеры

Квадратным уравнением называется уравнение вида ax ² + bx + c = 0, где а ¹ 0,  a, b, c - действительные числа. При а = 1 уравнение имеет вид х ² + px + q = 0 и называется приведенным.

Решение квадратного уравнения представим в таблице.

ax^2+ bx + c = 0	x ^2+ px + q = 0
, если b = 2k, то	если p = 2k, то

Замечание. Иногда для нахождения корней квадратного уравнения используют формулы Виета.

Формулы Виета (х₁ и х₂ - корни уравнения)

ax^2+ bx + c = 0	x ^2+ px + q = 0
x1 + x2 = - b/a ; x1x2 = c/a	x1 + x2 = - p ; x1x2 = q

Решения неполного квадратного уравнения.

ax ^2+ bx = 0	ax ^2+ c = 0	ax ^2= 0
		x = 0

Пример. Решить уравнение х ²- 3ах + а ²=0, если его корни х₁ и х₂ удовлетворяют условию х₁²+ х₂² = 112, а Î R.

Решение. Найдем значение параметра "а", используя формулу Виета и условие.

Возведем в квадрат обе части уравнения (1) и учитывая (3), получим

112 + 2а ²= 9а ², откуда а = ± 4.

Проверка показывает, что оба значения удовлетворяют данному уравнению.

1. Найдем решение уравнения:

1). при a = 4 х^2- 12х + 16 = 0, ,

2) при a = - 4 х^2+ 12x - 16 = 0, .

Ответ.

,