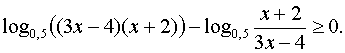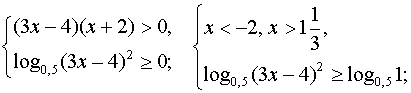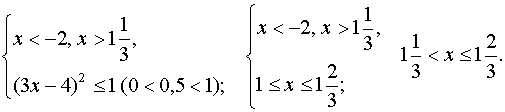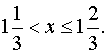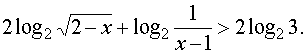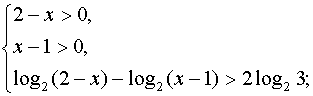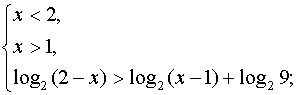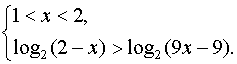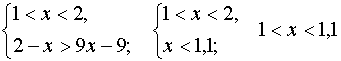2.2.2. Cведение неравенств к виду log a f(x) > log a g(x) (<, ³, £) с помощью свойств логарифмов по одному основанию. Если неравенства содержат логарифмы по одному основанию, то для приведения их к виду log a f(x) > log a g(x) (<, ³, £) используются следующие свойства логарифмов: logb a + logb c = logb (ac), где a > 0; c > 0; b > 0, b ¹ 1, logb a – logb c = logb (a/c), где a > 0; c > 0; b > 0, b ¹ 1, m logb a = logb a^m, где a > 0; b > 0, b ¹ 1; mÎR. Пример 1. Решить неравенство Решение. Учитывая область определения неравенства и применяя формулу логарифма частного, получим систему неравенств, эквивалентную данному неравенству.
Ответ.
Пример 2. Решить неравенство Решение. Применим формулу логарифма степени, формулу перехода к новому основанию логарифма и учтём область определения неравенства. Решим систему Так как функция y = log2 t возрастает (2 > 1), получим . Ответ. 1 < х < 1,1.