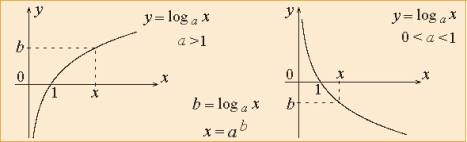2.1.1. Уравнения вида log_a x = b, a > 0, a ≠ 1.

Для решения уравнения применяются определение логарифма и свойства логарифмической функции y = log_a x.

Областью определения логарифмической функции y = log_ax являются все положительные числа. Множеством значений логарифмической функции являются все действительные числа. Логарифмическая функция монотонна на промежутке (0; +¥).

Применим к уравнению log_a x = b, a > 0, a ¹ 1 теорему о корне уравнения.

Теорема. Если b – любое из значений, принимаемых монотонной функцией на некотором промежутке, то уравнение f(x) = b имеет единственный корень в этом промежутке.

Теорему в применении к логарифмической функции иллюстрирует рисунок.

Таким образом, при любом действительном значении b уравнение имеет единственный корень. Для нахождения корня надо воспользоваться определением логарифма: x = a^b.

Пример. Решить уравнение

log₂ x = 3.

Решение. Область определения уравнения x > 0. По определению логарифма x = 2³, x = 8 принадлежит области определения уравнения.

Ответ: x = 8.