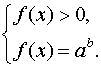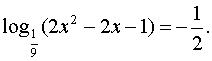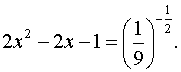2.1.2. Уравнения вида log_a f(x) = b, a > 0, a ≠ 1.

Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x). Уравнение равносильно следующей системе

Обычно область определения находится отдельно, и после решения уравнения f(x) = a^b проверяется, принадлежат ли его корни области определения уравнения.

Пример. Решить уравнение

Решение. Область определения уравнения находится из неравенства 2х² – 2х – 1 > 0. Воспользуемся определением логарифма:

Применим правила действий со степенями, получим 2х² – 2х – 1 = 3. Это уравнение имеет два корня х = –1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х² – 2х – 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями.

Ответ. х₁ = –1, х₂ = 2.