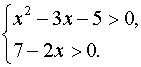|
2.2.1. Уравнения
вида
loga f(x)
= loga g(x)
, а > 0, а ¹ 1.
На основании свойства монотонности логарифмической
функции заключаем, что f(x) = g(x). Переход
от уравнения loga f(x) = loga g(x) к уравнению f(x) = g(x) называется потенцированием. Нужно
отметить, что при таком переходе может нарушиться равносильность уравнения. В
данном уравнении f(x) > 0,
g(x) > 0, а в полученном после потенцирования эти функции
могут быть как положительными, так и отрицательными. Поэтому из найденных
корней уравнения f(x) = g(x) нужно отобрать те, которые
принадлежат области определения данного уравнения. Остальные корни будут
посторонними. Пример. Решить
уравнение log3 (x2 – 3x – 5) = log3 (7 – 2x). Решение. Область
определения уравнения найдётся из системы неравенств Потенцируя данное уравнение, получаем х2 – 3х – 5 = 7 – 2х,
х2 – х – 12 = 0, откуда х1
= –3, х2 = 4. Число 4 не удовлетворяет системе
неравенств. Ответ. х = –3. |
|
|