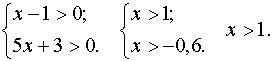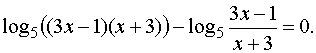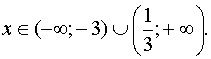2.2.2. Cведение уравнений к виду log _a f(x) = log _a g(x)

с помощью свойств логарифмов по одному основанию.

Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log _a f(x) = log _a g(x) используются следующие свойства логарифмов:

• log_b a + log_b c = log_b (ac), где a > 0; c > 0; b > 0, b ¹ 1,
• log_b a – log_b c = log_b (a/c), где a > 0; c > 0; b > 0, b ¹ 1,
• m log_b a = log_b a ^m, где a > 0; b > 0, b ¹ 1; mÎR.

Пример 1. Решить уравнение

log₆ (x – 1) = 2 – log₆ (5x + 3).

Решение. Найдём область определения уравнения из системы неравенств

Применяя преобразования, приходим к уравнению

log₆ (x – 1) + log₆ (5x + 3) = 2,

log₆ ((x – 1)(5x + 3)) = 2, далее, потенцированием, к уравнению

(х – 1)(5х + 3) = 36, имеющему два корня х = –2,6; х = 3. Учитывая область определения уравнения, х = 3.

Ответ. х = 3.

Пример 2. Решить уравнение

Решение. Найдём область определения уравнения, решив неравенство (3x – 1)(x + 3) > 0 методом интервалов.

Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log₅ (x + 3) ² = 0. По определению логарифма

(х + 3) ² = 1, х = –4, х = –2. Число х = –2 посторонний корень.

Ответ. х = –4.

Пример 3. Решить уравнение

log₂ (6 – x) = 2log₆ x.

Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 – x = x², откуда х = –3, х = 2. Число х = –3 посторонний корень.

Ответ. х = 2.