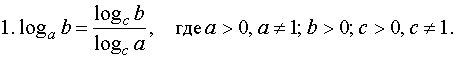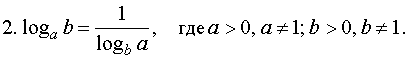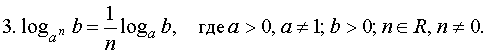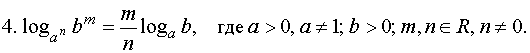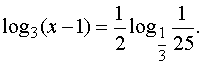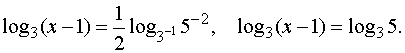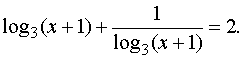|
2.2.3. Уравнения
вида Alog a f(x) + Blog b g(x) + C = 0. Метод
потенцирования применяется в том случае, если все логарифмы, входящие в
уравнение, имеют одинаковое основание. Для приведения логарифмов к общему
основанию используются формулы:
Пример 1. Решить уравнение
Решение. Область
определения уравнения 1 < x < 2. Используя
формулу (3), получим
Так как 3 = log28, то на области определения
получим равносильное уравнение (2–x)/(x–1)
= 8, откуда x
= 10/9. Ответ. x = 10/9. Пример 2. Решить уравнение
Решение. Область определения
уравнения x
> 1. Приведём
логарифмы к основанию 3, используя
формулу (4).
Ответ. х = 6. Пример 3. Решить уравнение
Решение. Область определения
уравнения x
> –1, x ¹ 0. Приведём логарифмы к
основанию 3, используя формулу (2).
Умножим обе части уравнения на log 3(x + 1) ¹ 0 и перенесем все слагаемые в левую часть уравнения. Получим (log 3(x + 1)–1)2 = 0, откуда log 3(x + 1) = 1 и x = 2.Ответ. x = 2. |
|
|