2.3.1. Уравнения вида

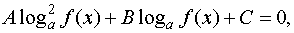
где a > 0, a ¹ 1, A, В, С – действительные числа.

Пусть t = log_a f(x), tÎR. Уравнение примет вид t² + Bt + C = 0.

Решив его, найдём х из подстановки t = log_a f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.

Пример 1. Решить уравнение lg ² x – lg x – 6 = 0.

Решение. Область определения уравнения – интервал (0; ¥).Введём новую переменную t = lg x, tÎR.

Уравнение примет вид t ² – t – 6 = 0. Его корни t₁ = –2, t₂ = 3.

Вернёмся к первоначальной переменной lg x = –2 или lg x = 3,

х = 10 ^–2 или х = 10 ³. Оба значения x удовлетворяют области определения данного уравнения (х > 0).

Ответ. х = 0,01; х = 1000.

Пример 2. Решить уравнение

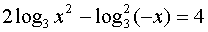
Решение. Найдём область определения уравнения

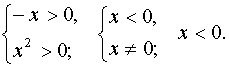
Применив формулу логарифма степени, получим уравнение

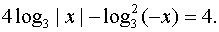
Так как х < 0, то | x | = –x и следовательно

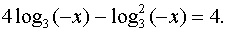
Введём новую переменную t = log₃ (–x), tÎR. Квадратное уравнение

t ² – 4t + 4 = 0

имеет два равных корня t_1,2 = 2. Вернёмся к первоначальной переменной log₃ (–x) = 2, отсюда –х = 9, х = –9. Значение неизвестной принадлежит области определения уравнения.

Ответ. х = –9.