2.3.2. Уравнения вида

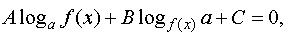
где a > 0, a ¹ 1, A, В, С – действительные числа , A¹0, В¹0.

Теория и пример.

Уравнения данного вида приводятся к квадратным умножением обеих частей его на log_a f(x) ¹0. Учитывая, что log_a f(x)× log_f(x) a=1

(свойство log_b a = 1/ log_a b), получим уравнение

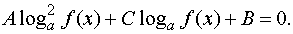
Замена log_a f(x)=t, tÎR приводит его к квадратному

At² + Ct + B = 0.

Из уравнений log_a f(x)= t₁ , log_b f(x)= t₂ найдем значения x и выберем среди них принадлежащие области определения уравнения:

f(x) > 0, f(x) ¹1.

Пример. Решить уравнение

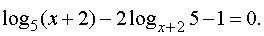
Решение. Область определения уравнения находим из условий x+2>0, x+2 ¹ 1, т.е. x >–2, x ¹ –1.

Умножим обе части уравнения на log₅ (x+2) ¹0, получим

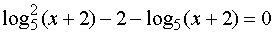
или, заменив log₅ (x+2) = t, придем к квадратному уравнению

t ² – t – 2 = 0, t₁ = –1, t₂ =2.

Возвращаемся к первоначальной переменной:

log₅ (x+2) = –1, x+2 = 1/5, x = –9/5,

log₅ (x+2) = 2, x+2 = 25, x = 23.

Оба корня принадлежат области определения уравнения.

Ответ: x = –9/5, x = 23.