3.2.Уравнения вида

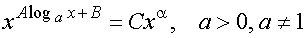
Теория и примеры

Область определения уравнения – интервал (0, ¥). Прологарифмируем обе части уравнения по основанию a, получим

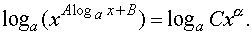
Применим формулы логарифма степени и логарифма произведения

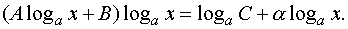
Введем новую переменную t=log_a x , tÎR. Решив квадратное уравнение At² + (B–a)t–log_a C=0, найдем его корни t₁ и t₂. Значение x найдем из уравнений t₁ = log_a x и t₂=log_a x и выберем среди них принадлежащие области определения уравнения.

Пример 1. Решить уравнение

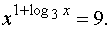
Решение. Область определения уравнения х > 0. Так как при х > 0 обе части уравнения положительны, а функция y = log₃ t монотонна, то

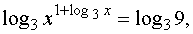
(1 + log₃ x) log₃ x = 2.

Введём новую переменную t, где t = log₃ x, tÎR.

(1 + t) t = 2, t ² + t – 2 = 0, t₁ = –2, t₂ = 1.

log₃ x = –2 или log₃ x = 1,

x = 1/9 или х = 3.

Ответ. х = 1/9; х = 3.

Пример 2. Решить уравнение

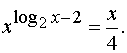
Решение. Область определения уравнения х >1. Обе части уравнения положительны, прологарифмируем их по основанию 2, получим

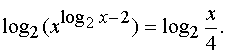
Применим формулы логарифма степени и логарифма частного:

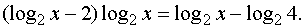
Введем новую переменную t=log₂x, получим квадратное уравнение

t² - 3t + 2 = 0,

t₁ = 2, t₂ = 1, тогда log₂ x = 2 или log₂ x =1.

Ответ. x = 4, x = 2.