2.1.1. Неравенства вида a x >b ( < , ≥ , ≤ ) , a > 0, a ≠ 1
Теория и примеры.
1. Пусть b ≤ 0.
Множеством значений показательной функции y = a x являются все положительные числа. Поэтому при b<0 или при b = 0 неравенства a x < b и a x Ј b не имеют решений, а неравенства a x > b и a x і b выполняются при любых действительных значениях переменной x.
2. Пусть b > 0.
Представим число b в виде степени числа а. Если это не удается сразу, то применим основное логарифмическое тождество
.
Неравенство примет вид
Учитывая монотонность показательной функции, перейдем к равносильному неравенству x > log a b (при a>1) или x < log a b (при 0<a<1).
Пример 1. Решить неравенство 2x+1 Ј 3.
Решение. Область определения неравенства: xОR. Представим число 3 в виде степени с основанием 2, используя основное логарифмическое тождество
alogam = m.
Неравенство примет вид
.
Так как a = 2 >1, то, решая эквивалентное неравенство,
,		получим		.
Ответ.	.
Пример 2.Решить неравенство
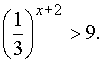
Решение. Область определения неравенства: xОR. На основании правил действий со степенями приведем обе части неравенства к основанию 3:
.
При основании, большем единицы (a = 3), показательная функция монотонно возрастает. Неравенство эквивалентно неравенству –x–2>2, откуда x < – 4.
Ответ. x < – 4.
Пример 3. Решить неравенство
Решение. Область определения неравенства:
Приведем обе части неравенства к основанию 2:
В силу возрастания показательной функции с основанием, большим единицы, получим эквивалентное неравенство
которое выполняется при любых значениях переменной из области определения.
Ответ. x Ј 2/3.