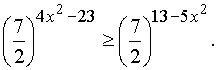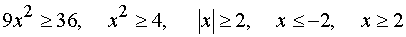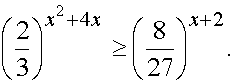2.1.2. Неравенства вида

a ^f(x) >a ^g(x) ( < , ≥ , ≤ ) , a > 0, a ≠ 1

Теория и примеры.

Решение неравенств этого типа основано на свойстве монотонности показательной функции.

Если a >1, то функция y = a ^x монотонно возрастает и данное неравенство равносильно неравенству

Если 0 < a <1, то функция y = a ^x монотонно убывает и данное неравенство равносильно неравенству

f(x) < g(x).

Пример 1. Решить неравенство

Решение. Область определения неравенства: xОR. На основании свойства монотонности показательной функции получим при основании a >1 равносильное неравенство:

Решим это неравенство.

Ответ. x ≤ –2 и x ≥ 2.

Пример 2. Решить неравенство

Решение. Область определения неравенства: xОR. Основание a = 2/3, a <1, функция y =(2/3)^t – монотонно убывающая. Переходим к равносильному неравенству

x²+4x ≤ 3x+6, или x²+x – 6 ≤ 0.

Решаем квадратное неравенство. Находим корни многочлена x²+x – 6, это x₁ = – 3, x₂ =2. Построим параболу , являющуюся графиком функции y = x²+x – 6 и выберем нужный по условию интервал.

Ответ. –3 ≤ x ≤ 2.