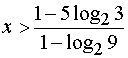2.1.3. Неравенства вида a f(x) >b g(x) ( < , ≥ , ≤ ) , a > 0, a ≠ 1; b >0, b ≠ 1
Теория и примеры.
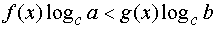
Представлением числа b степенью числа a это неравенство приводится к простейшему неравенству вида a f(x) > a g(x). 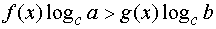Рассматриваемые в этом пункте неравенства можно также решать логарифмированием обеих частей по любому основанию c (с > 0, c ≠ 1 ), учитывая свойство монотонности логарифмической функции: при 0 < c < 1получим неравенство (знак неравенства меняется на противоположный); при c > 1 получим неравенство (знак неравенства сохраняется).
Пример 1. Решить неравенство
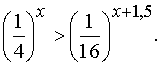
Решение. Область определения неравенства: xОR.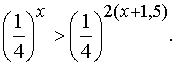
Так как a =1/4 <1, то показательная функция убывающая. Переходим к равносильному неравенству x < 2x + 3. Решим его и получим x > –3.
Ответ. x > –3.
Пример 2. Решить неравенство.
Решение. Область определения неравенства: xОR.
Логарифмируем обе части неравенства по основанию 2. Так как a = 2>1, то знак неравенства сохраняется. Получим
(x–1)log 2 2 < (2x – 5)log 23, или x–1 < 2x log 2 3 – 5 log 2 3.
Перенесем влево слагаемые, содержащие переменную x:
x(1– 2 log 2 3) < 1–5 log23.
Перед тем, как разделить обе части неравенства на число 1– 2 log 2 3, выясним его знак:
2 log 2 3= log 2 9 > 1, тогда 1– log 2 9 < 0.
Учитывая это, получим
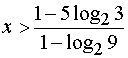
Ответ.