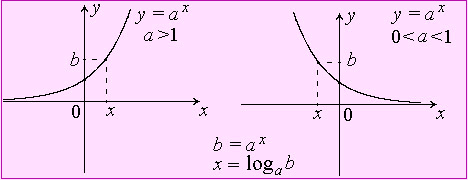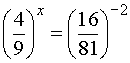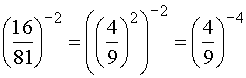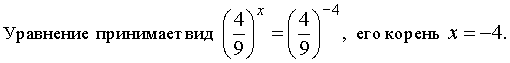Теория и примеры.

Множеством значений показательной функции y = a ^x являются все положительные числа. Поэтому при b<0 или при b = 0 уравнение не имеет решений.

Показательная функция монотонна на промежутке

^.

Применим к ней следующую теорему о корне уравнения:

Теорема. Если b -любое из значений, принимаемых монотонной функцией f(x) на некотором промежутке, то уравнение

имеет единственный корень в этом промежутке.

Теорему в применении к показательной функции иллюстрирует рисунок.

Для ознакомления с доказательством теоремы щелкните мышью на слове "доказательство".

Таким образом, при b > 0 уравнение имеет единственный корень. Этот корень называется логарифмом числа b по основанию a и обозначается так:

.

Замечание. При решении конкретного уравнения понятие логарифма может и не понадобиться, если число b удастся записать как степень числа a с действительным показателем: при b = a ^c уравнение a ^x = b принимает вид a ^x = a ^c и из единственности корня следует, что x = c.

Пример 1. Решить уравнение

5 ^x=3.

Решение. Область определения уравнения: xОR.

Так как b = 3>0, то уравнение имеет единственное решение - логарифм числа 3 по основанию 5.

Ответ. x=log₅3.

Пример 2. Решить уравнение

Решение. Область определения уравнения: xОR .

Так как стоящее в правой части число b > 0, то уравнение имеет единственное решение.

Приведем число b к основанию 4/9, используя правила действий со степенями:

Ответ. x = – 4.