Примеры.

Пример 1. Решить неравенство

.

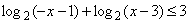Решение. Найдем область определения неравенства:

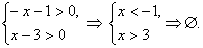
Область определения пуста.

Ответ. Неравенство не имеет решений.

Пример 2. Решить уравнение  

.

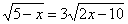Решение. Найдем область определения уравнения:

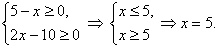
Область определения состоит из одной точки.

Подстановкой в уравнение можно убедиться, что  x = 5 – решение.

Ответ. x = 5.

Пример 3. Решить уравнение

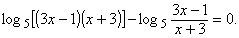
Решение. Найдем область определения уравнения, решая методом интервалов систему:

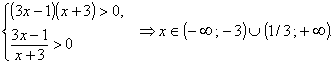
Выполним в левой части уравнения упрощающие преобразования, используя свойства логарифмов:

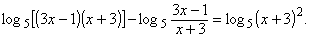
Решаем уравнение

log₅(x+3)² = 0,

являющееся следствием исходного уравнения, но имеющее другую, более широкую область определения.

Имеем:

(x+3)² = 1,  x+3 = ±1,

 откуда x = – 4  и  x = – 2.  Решением исходного уравнения является только  x = – 4  ,  так как значение  x = – 2    не входит в его область определения.

Ответ. x = – 4.

Не всегда обязательно решать неравенства, задающие область определения. Иногда достаточно проверить их выполнение для найденных в процессе решения значений переменной.

Пример 4. Решить уравнение   cosec x  tg² x = 0.

Решение. Запишем уравнение в виде

.

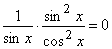Область определения уравнения определяется неравенствами sin x ¹ 0, cos x¹ 0. После упрощения получим  уравнение

sin x = 0

с более широкой областью определения. Его решения в область определения исходного уравнения не попадают.

Ответ. Уравнение не имеет решений.

Пример 5. Решить неравенство

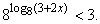
Решение. Область определения неравенства находится из условия 3 + 2x > 0.  Применяя определение логарифма, получим неравенство

3 + 2x<3 .

 Его область определения – все действительные числа. Заданное неравенство может быть заменено системой

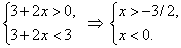
Ответ. xÎ (-3/2 , 0).

Пример 6. Решить уравнение

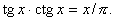
Решение. Область определения уравнения x ¹ pk/2, kÎ Z.

При этих предположениях уравнение преобразуется в уравнение

1= x/p,

имеющее областью определения все x Î R. Его единственное решение x = p не входит в область определения исходного уравнения.

Ответ. Уравнение не имеет решений.

Пример 7. Решить неравенство 

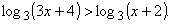
Решение. Область определения неравенства: xÎ (– 4/3; + ¥). На основании монотонности функции логарифм отбрасываем логарифмы и переходим к неравенству

3x + 4 > x + 2,

имеющему областью определения все x Î R. Его решения: x > -1, множество решений полностью содержит область определения исходной задачи.

Ответ.  xÎ(-4/3 ; + ¥).

Пример 8. Решить неравенство

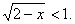
Решение. Область определения неравенства: xÎ ( – ¥; 2]. Возведем обе части уравнения в квадрат (они неотрицательны, следовательно, придем к равносильному неравенству). Для нового неравенства

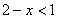
областью определения является вся действительная ось. Его решения x >1 лишь частично входят в область определения исходной задачи.

Ответ. xÎ ( 1; 2].

Пример 9. Решить уравнение

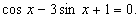
Решение. Область определения уравнения: xÎR. Выразим функции cosx  и  sinx через функцию tg(x/2):

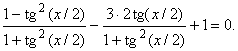
Введение функции  tg(x/2) сужает область определения уравнения, так как не могут рассматриваться точки x = p + 2kp (k - целое). Выбранный метод решения приводит к необходимости рассматривать два случая:

1. x = p + 2kp (k - целое). Непосредственная подстановка этих значений переменной в уравнение убеждает, что это – решения.

2.      x ¹ p + 2kp (k - целое). Вводя переменную t = tg(x/2) приходим к линейному уравнению

2 – 6t = 0,

откуда t = 1/3, то есть tg(x/2) = 1/3 и x = 2arctg(1/3) + 2kp,  kÎ Z.

Объединим найденные решения.

Ответ. x = p + 2kp,  x = 2arctg(1/3) + 2kp,  kÎ Z.

Пример 10. Решить уравнение

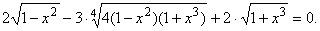
Решение. Область определения уравнения: xÎ [– 1; 1]. Записав его в форме

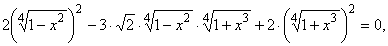
замечаем, что это уравнение имеет вид

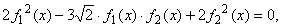
то есть является однородным относительно функций

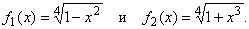
Стандартный прием решения однородных уравнений, состоит в  делении уравнения на f₂²(x) и сведении его к квадратному введением новой переменной

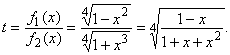
Однако, такие действия становятся возможными лишь при дополнительном предположении

1 + x³ ¹ 0,

сужающем область определения уравнения.

Рассмотрим 2 случая:

1) x = – 1. Непосредственная подстановка этого значения переменной в уравнение убеждает, что это – решение.

2) x ¹ – 1. Уравнение сводится к квадратному

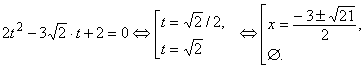
Одно из значений не принадлежит области определения исходного уравнения.

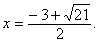
Замечание. Данное уравнение можно решать вынесением общего множителя за скобки, но это повлечет более громоздкие выкладки.