Примеры.

Пример 1. Решить уравнение

.

Решение. Найдем область определения:   x + 1³0 Þ x ³ –1.  Переписав уравнение в виде

и учитывая область значений функции «арифметический квадратный корень», обозначаемой знаком радикала:

,

делаем вывод:  x + 1 = 0,  иначе правая и левая части имели бы разные знаки.

Ответ. x = –1.

Пример2. Решить уравнение

.

Решение. Подкоренное выражение – квадрат двучлена. Поэтому область определения :xÎ(– ¥, + ¥).  Выполнив преобразования в левой части уравнения

,

получаем:

| 3x – 1 | = 1–3x.

Так как значения функции «модуль» неотрицательны, должно быть

1–3x ³ 0.

По определению модуля все решения последнего неравенства будут и решениями исходного уравнения, которое можно записать так:

| 1 – 3x | = 1–3x.

Ответ. x £ 1/3.

Пример 3. Решить неравенство

Решение. Область определения:  xÎR.  Перепишем неравенство в виде

|1- x| >1- x.

Так как значения функции «модуль» неотрицательны, строгое неравенство будет выполнено при всех x, таких что 1- x <0 .

Ответ. x >1.

Пример 4. Решить уравнение 

.

Решение. Область определения задается неравенством 2x² –1 ³ 0. Так как функция «арифметический квадратный корень» принимает только неотрицательные значения, имеем:

и  поэтому  равенство в исходном уравнении можно получить лишь при условии

.

Ответ.

Пример 5 . Решить неравенство

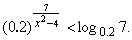
Решение. Область определения неравенства:

xÎ(- ¥ ; –2) È (- 2; 2) È (2; + ¥).

Заметим, что левая часть не может быть отрицательной, так как значения показательной функции  y = a ^t  строго положительны, а в правой части стоит отрицательное число, так как  log _a b < 0, если одно из положительных чисел a, b больше единицы, а второе - меньше).

Ответ. Неравенство не имеет решений.

Пример 6. Решить неравенство

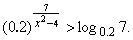
Решение. Область определения неравенства

xÎ(- ¥ ; –2) È (- 2; 2) È (2; + ¥).

Поскольку левая часть неравенства положительна, а в правой части стоит отрицательное число, решениями будут все значения переменной x, входящие в область определения.

Ответ. xÎ(- ¥ ; –2) È (- 2; 2) È (2; + ¥).

Пример 7. Решить неравенство

.

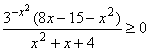Решение. Дискриминант квадратного трехчлена, стоящего в знаменателе, отрицателен. Поэтому при любых  x  знаменатель больше нуля, область определения неравенства:  xÎ(- ¥ ; + ¥). Множитель 3^–x также положителен  и данное неравенство эквивалентно неравенству

8x – 15 – x² ³ 0.

Перепишем его в виде –(x – 3)(x – 5) ³ 0 и решим его методом интервалов.

Ответ. xÎ [3,5].

Пример 8. Решить уравнение

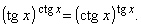
Решение. Область определения уравнения задается неравенствами tg x >0, ctg x >0 (только в этом случае могут рассматриваться показательно-степенные функции (tg x)^{ctg x}  и  (ctg x)^{tg x}. Заметим, что

tg x = 1/ctg x,

откуда следует, что

tg x >1 Û ctg x <1  и  tg x <1 Û ctg x >1.

Поскольку положительная степень числа, большего единицы, является числом  большим единицы, а положительная степень числа, меньшего единицы, является числом меньшим единицы, левая часть уравнения может равняться правой только в случае

tg x = ctg x = 1.

Ответ. x = p/4 + kp, k Î Z.