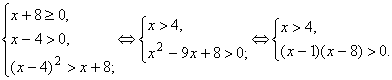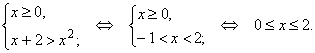Примеры.

Пример 1. Решить уравнение

Решение. Область определения:  xÎR.  Приведём левую и правую части уравнения к одному основанию:

Из монотонности показательной функции следует, что  3x -7 = 3 -7x  и  x = 1.

Ответ. x = 1.

Пример 2. Решить уравнение 

Решение. Область определения уравнения :  x Î(- ¥ ; 5).  С использованием свойств логарифмов уравнение может быть приведено к виду

Из монотонности логарифмической функции  следует:

то есть  x  является корнем квадратного уравнения  x²-16x-36 = 0.  Из двух его корней  x₁=18  и  x₂= – 2,  учитывая область определения исходного уравнения, оставляем один.

Ответ.  x= -2.

Пример 3 . Решить неравенство

.

Решение. Область определения неравенства:  xÎR.  Перепишем неравенство в виде

и разделим обе части на общий множитель, принимающий только положительные значения (знак неравенства сохраняем). Получим

Отсюда

и  x > log_3/4 5 (используем монотонность функции  y = a^x   с основанием  a = 3/4; она монотонно убывает, поэтому знак неравенства меняем на противоположный).

Ответ. x > log_3/4 5.

Пример 4. Решить неравенство 

Решение. Область определения неравенства: xÎ (– 4/3; + ¥). Функция y = log_1/3 t  монотонно убывает, поэтому  3x+4 < x+2,  откуда x < -1.

Ответ.  xÎ(-4/3 ; -1).

Пример 5. Решить неравенство

.

Решение. Область определения неравенства:  xÎ [– 8; + ¥).  Так как  правая часть неравенства принимает только неотрицательные значения, по смыслу неравенства должно быть  x – 4 > 0. Поэтому можно применить метод возведения в квадрат (функция y = t²  монотонно возрастает при неотрицательных значениях переменной t).

Неравенство эквивалентно системе

Ответ. xÎ (8; + ¥).

Пример 6. Решить неравенство

Решение. Область определения неравенства: xÎ [– 2, + ¥). Рассмотрим два случая:

а) x < 0. Поскольку левая часть неравенства может принимать только неотрицательные значения, неравенство справедливо для всех отрицательных значений  x, входящих в область определения. Отсюда –2 £ x < 0.

б) x ³ 0. Пользуясь монотонным возрастанием функции  y = t ² при t ³ 0, применяем метод возведения в квадрат, сохраняя знак неравенства.

Рассматриваем систему

Объединяя решения, полученные в случаях а) и б), получаем .

Ответ. –2 £ x < 2  или, в другой форме,  xÎ [– 2; 2).

Пример 7. Решить неравенство

Решение. Область определения неравенства: xÎ (0, + ¥). Воспользуемся монотонным возрастанием функции lg t :  t₁ < t₂ Û lg t₁ < lg t₂. Отсюда следует, что вместо заданного неравенства можно решать эквивалентное ему неравенство, полученное логарифмированием обеих его частей,

Имеем

Остается еще раз воспользоваться монотонностью логарифмической функции.

Ответ. 10 ^{– 2} < x < 10 ².

Пример 8. Решить неравенство

Решение. Область определения неравенства:  x < 1, x ¹ – 1.

Знак дроби определяется знаками числителя и знаменателя. Перемена знака в знаменателе происходит в точке x = –1. Знак разности в числителе всегда совпадает со знаком разности (1 – x) – (x² + x +1), так как функция «арифметический квадратный корень» – монотонно возрастающая, то есть

Вместо заданного неравенства можно рассматривать неравенство

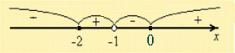
Применим метод интервалов.

Учитывая область определения, выпишем ответ.

Ответ. xÎ [– 2; – 1)È[0; 1].
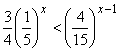