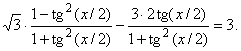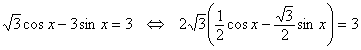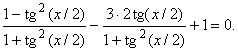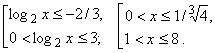Примеры. Список задач

Пример 1. Решить уравнение

.

Решение. Область определения уравнения:  xÎR. Заметим, что x входит в заданное уравнение в составе выражений  9^{2x +3}   и  3^{2x + 1}. Нетрудно видеть, что оба эти выражения могут быть представлены через одно, например, через  3^2x+1.  Действительно,  9^{2x +3} = 9²×9^2x+1 = 9²×3^2×(2x+1) = 9²×(3^2x+1)².  Уравнение примет вид

81×(3^2x+1)² = 6×3^2x+1 + 7.

Достаточно ввести новую переменную

t =

,

чтобы получить квадратное уравнение

81t² – 6t –7 = 0.

Из двух корней  t = 1/3  и  t = –7/27  рассматриваем только положительный, так  показательная функция отрицательных значений принимать не может.

 Для возвращения к исходной переменной, решаем уравнение

= 1/3,

откуда 2x +1= –1 и x = –1.

Ответ. x = –1 .

Замечание. Можно было выбрать и такую переменную: t= 3^2x. Но получаемое в этом случае квадратное уравнение  9³×t² – 18×t –7 = 0  имеет большие, менее удобные для вычислений коэффициенты.

Пример 2. Решить уравнение 

.

Решение. Областью определения уравнения является интервал (- ¥ ; + ¥), так как дискриминант квадратного трехчлена, записанного под корнем, отрицателен. Запишем уравнение в виде

и введем переменную

t =

Получим квадратное уравнение

t² – 5t –24 = 0.

Рассматривая положительный корень  t = 8, для возвращения к исходной переменной решаем уравнение

8 =

Имеем  x² + 5x + 28 = 64,  откуда   x = 4 и x = -9.

Ответ. x = 4 и x = -9.

Пример 3. Решить уравнение

Решение. Область определения уравнения:  xÎR. Переменная x входит в него в функциях  cosx  и  sinx. Заметим, что после деления уравнения на  cosx  мы придем к равносильному уравнению, в котором  x будет встречаться только в одной функции tg x

Заметим, что при делении мы  не потеряли решений; в данном уравнении не может быть  cosx = 0,  иначе для тех же  x  из уравнения следовало бы  sin x = 0,  что невозможно. Относительно новой переменной

t =

получено линейное уравнение

t = 0.

Находим  t  и решаем уравнение

для возвращения к исходной переменной.

Ответ.

Пример 4. Решить уравнение

Решение. Область определения уравнения: xÎR. Уравнение можно свести к квадратному, выразив функции cosx  и  sinx через функцию tg(x/2), а также к линейному, преобразовав левую часть для применения формулы косинуса суммы или синуса разности. Рассмотрим обе возможности.

В первом случае будем иметь:

Введение функции tg(x/2) изменяет область определения уравнения. Подставляя в уравнение значения x = p + 2kp (k - целое) убеждаемся, что решения при этом не будут потеряны. Вводя переменную

t =

получим уравнение

1 – t²

1 + t²

     6t  ^a

  1+ t²

= 3

t² + 6t +

Найдем его корни (избавляясь от иррациональности в знаменателе):

t = –1    и    t = –2 +

Для возвращения к исходной переменной решим уравнения

= – 1    и

Получим

Во втором случае выполним преобразования в левой части уравнения:

и запишем его в виде

Имеем соответственно

Получено линейное уравнение

t = 3

относительно новой переменной

t =

  или   t =

Находим его единственное решение

t =

и для возвращения к исходной переменной решаем простейшее тригонометрическое уравнение

Имеем

Ответ.

Выпишем ответ во всех трех найденных формах.

Пример 5. Решить уравнение

Решение. Область определения уравнения: xÎR. Сведем уравнение к квадратному, выразив функции cosx  и  sinx через функцию tg(x/2):

Введение функции  tg(x/2) изменяет область определения уравнения, так как не могут рассматриваться точки x = p + 2kp (k - целое). Выбранный метод решения приводит к необходимости рассматривать два случая:

1. x = p + 2kp (k - целое). Непосредственная подстановка этих значений переменной в уравнение убеждает, что это – решения.
2. x ¹ p + 2kp (k - целое). Вводя переменную

t =

получим уравнение

1 – t²

1 + t²

     6t  ^a

  1+ t²

+ 1= 0

Û

2 – 6t = 0.

Находим

t = 1/3.

Возвращаясь к исходной переменной, решаем уравнение

=1/3.

Ответ. x = p + 2kp,  x = 2arctg(1/3) + 2kp,  kÎ Z.

Пример 6. Решить неравенство

.

Решение. Область определения уравнения:  xÎR. Если заметить, что 9^x = (3^x)²,  6^x  = 3^x× 2^x,  2^2x+1 = 2× (2^x)² ,  то можно увидеть, что переменная x участвует в неравенстве только в составе двух функций:  3^x  и  2^x . Перепишем неравенство, выделив эти функции, и подумаем, нельзя ли его преобразовать так, чтобы в новое неравенство переменная входила в составе только одной функции:

Видим, что желаемого результата можно добиться делением неравенства на (2^x)² или на (3^x)² (заметим, что при всеx  значениях x  это положительные числа, знак неравенства сохраняем):

Введение переменной

t =

приводит к квадратному неравенству

t² + t –2 < 0.

Его решения:  – 2 < t < 1. В нашей задаче левое неравенство выполняется автоматически, поскольку показательная функция может принимать только положительные значения.

Для возвращения к исходной переменной решаем неравенство

< 1.

Значения показательной функции с основанием, большим единицы, меньше единицы при x < 0.

Ответ.  x < 0.

Замечание. Данное неравенство однородно относительно функций 3^x  и  2^x . Аналогично решаются задачи, однородные относительно любых двух функций, нужно только следить за тем, чтобы не потерять решения при делении на степень одной из этих функций (если она может равняться нулю).

Пример 7. Решить неравенство

Решение. Область определения неравенства: xÎ(0 , 1) È(1,+¥). Преобразовав

введем переменную

t =

Неравенство примет вид

1/t – t/2 + 7/6 ³ 0.

Приведем его к виду, удобному для применения метода интервалов:

6 – 3t² +7t

                               6t

­3(t –3)(t + 2/3)

         6t

Нанося на числовую прямую точки перемены знака дроби, найдем интервалы, на которых выполняется неравенство:

tÎ(– ¥, ­2/3] È (0, 3] .

Для возвращения к исходной переменной решаем неравенства

Ответ. 0 < x £ 1/4^1/3,  1 < x £ 8.

Пример 8. Решить уравнение 

.

Решение. Область определения уравнения:  x Î(0, + ¥). Переменная  x  встречается в степени и под логарифмом.  Переход к логарифмам обеих частей уравнения позволит добиться, чтобы  переменная  x  входила в новое уравнение только в выражении  lg x.  Действительно,  логарифмируя и используя свойства логарифма степени и логарифма произведения, получим

После введения переменной

t =

приходим к квадратному уравнению

2t²- 3t+1= 0,

корни которого:  t=1/2  и  t=1.  Возвращаясь к исходной переменной из уравнения

=1/2

получим x =10^1/2,  из уравнения

=1

 получим  x =10.

Ответ.