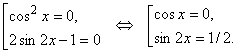Примеры.

Пример 1. Решить уравнение

.

Решение. Область определения:  x Î R.  Применим формулу

1+cos2x = 2 cos²x и вынесем за скобку общий множитель:

.

Нужно решить два более простых уравнения и объединить их решения:

Ответ.

Пример 2. Решить неравенство

Решение.  Область определения неравенства:

xÎ(-, -1)È(-1,+).

Перейдём к дроби, сравниваемой с нулём:

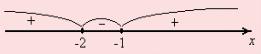
Применим метод интервалов (знак дроби меняется в точках –1 и –1/3):

Ответ. xÎ(-¥ , -1)È(-1/3,+ ¥)

Пример 3. Решить неравенство

.

Решение. Область определения неравенства:

x Î(-  ¥, 1) È (1, + ¥).

Каждый из множителей в числителе и в знаменателе может менять свой знак. Прежде всего необходимо провести дальнейшее разложение на множители и объединение или сокращение одинаковых множителей:

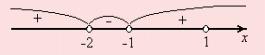
Множитель  (x + 1)  меняет знак в точке  x = – 1  (в которой он равен нулю), множитель  (x + 2) меняет знак в точке  x = – 2,  множитель  (x–1)²  знака не меняет, исключим его из рассмотрения. Дробь будет менять знак в двух точках:  x = – 1  и  x = – 2.  Нанесём их на числовую прямую. Тем самым определяются три интервала, на которых дробь сохраняет знак, а в точках, разделяющих эти интервалы, дробь меняет знак. Теперь легко расставить знаки, определив знак на крайнем правом интервале: для нашей дроби это  “+” . Далее знаки меняем автоматически при движении влево.

Осталось “выколоть” точку  x = 1,  не входящую в область определения, и исключить концы интервалов ввиду строгости неравенства.

Ответ. xÎ(- ¥ , -2) È(-1 , 1) È(1,+ ¥)

Пример 4. Решить неравенство

Решение. Область определения неравенства:

xÎ(- ¥ , -1) È(-1 ,1) È(1,+ ¥).

Найдём сначала решения строгого неравенства. Для применения метода интервалов множители  (x - 4)²   и  (x² - 1)²,  не меняющие знака, исключим из рассмотрения. Нанесём на числовую прямую точки перемены знака дроби: точку  x = 0,  в которой меняет знак множитель  x,  и точку  x = -1,  в которой меняет знак множитель  (x+1)³.  Расставим знаки дроби на полученных трёх интервалах:

Исключим точки, не входящие в область определения, и, возвращаясь теперь к исходному нестрогому неравенству, добавим точку  x = 4,  которая входит в область определения и  в которой равен нулю числитель дроби:

Ответ.  xÎ(-1 , 0] È{4}  

            Замечание. Если нанести на числовую прямую все точки, в которых обращаются в нуль числитель или знаменатель дроби, а не только точки, в которых происходит перемена  знака дроби, то автоматическая расстановка знаков после определения знака на одном из получившихся интервалов станет невозможна.

Пример 5. Решить неравенство

Решение. Область определения неравенства:

xÎ(- ¥ ; 1) È (1; + ¥).

Множитель  e ^x  знака не меняет, множители

меняют знаки в одной общей точке  x=1, следовательно, дробь в этой точке знака не меняет. Определяя знак дроби при  x >1, получим знак “–“.

Ответ.  xÎ(- ¥ ; 1)È(1; + ¥)

Пример 6. Решить неравенство

Решение. Область определения неравенства:

xÎ(0; 1) È (1; + ¥).

Преобразуем неравенство к виду, более удобному для применения метода интервалов.

В числителе и в знаменателе – монотонные функции. Следовательно, они меняют знак в тех точках, в которых они обращаются в нуль: числитель – в точке x = 2 ^{– 2} =1/4, знаменатель – в точке x =1. Нанесем эти точки перемены знака дроби на числовую прямую и определим знаки дроби на полученных интервалах: на крайнем правом интервале дробь положительна, знаки на остальных интервалах расставим автоматически.

Ответ.  xÎ(0; 1/4]È(1; + ¥)