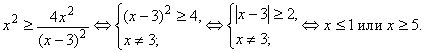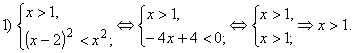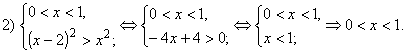Примеры.

Пример 1. Решить уравнение

|4 - x| + |x - 2| = 2.

Решение. Область определения уравнения: x Î R. Разобьём числовую прямую точками, в которых меняют знаки выражения, стоящие под знаком модуля, и расставим эти знаки на полученных интервалах. На каждом из интервалов раскрываем модули и решаем соответствующие уравнения. Имеем три задачи, каждая на своем подмножестве числовой прямой. Граничные точки будем включать и в левые, и в правые интервалы, поскольку решения в дальнейшем объединяются.

Ответ. xÎ[2; 4].

Пример 2. Решить уравнение

Решение. Область определения уравнения задается условием x ¹ p/2 + kp, kÎZ. Разобьем область определения на части, определяемые неравенствами

1) cosx – sinx ³ 0,  2) cosx – sinx < 0.

Не обязательно пытаться изобразить получаемые при этом множества на рисунке. Достаточно решать уравнение на каждом из них с учетом условий 1) или 2) соответственно.

Раскрывая модули, получаем две задачи.

Задача 1.

Преобразуем последнее уравнение:

Видно, что в этом случае sin x > 0. Введем переменную t = sin x и найдем положительный корень квадратного уравнения t² + t –1 = 0,

удовлетворяет условию | t | £ 1, следовательно, существуют решения уравнения sin x = t.

Проверим выполнение условия cosx – sinx ³ 0:

Учитывая, что sin x > 0, делаем вывод: выполнение условия эквивалентно выполнению неравенства cosx > 0:Следовательно,

Задача 2.

Преобразуем последнее уравнение:

Проверим выполнение условия cosx – sinx < 0: при cos x = 1 его выполнение невозможно, при sin x = 0 имеем cos x < 0. Отсюда

Ответ.

             Тождества  

 связывают уравнения и неравенства, содержащие модули, с иррациональными уравнениями и неравенствами. Отметим, что иногда путь решения, связанный не с раскрыванием модулей, а с использованием возведения в квадрат, оказывается более коротким. При этом используются следующие утверждения.

,   .

Пример 3. Решить неравенство

Решение. Область определения неравенства: xÎR.

Способ 1.  Разобьём числовую прямую точкой  x = 3/2, в которой меняет знак выражение  2x – 3, стоящее под знаком модуля, на два интервала и решим две задачи:

Теперь нужно объединить решения.

Способ 2. Возведем обе части уравнения в квадрат. Так как они неотрицательны, придем к равносильному неравенству

Тогда  4x² – 12x – 16 ³ 0,  x² – 3x – 4 ³ 0,  (x – 4)(x + 1) ³ 0.

Способ 3. Введем новую переменную t = 2x – 3 и решим неравенство

| t | ³ 5

геометрически: | t | есть расстояние от точки t до нуля на числовой оси.

Получили: t £ ­5 или  t ³ 5 , 2x – 3  £ – 5 или 2x – 3 ³ 5,  2x £ –2 или 2x ³ 8,  x £ –1 или x ³ 4.

Ответ. xÎ( – ¥; – 1]È[4; + ¥).

Замечание. Преимущества второго способа в данной задаче были бы сомнительны, если бы сложнее вычислялись корни квадратного уравнения, при первом способе решения решаются линейные уравнения.

Пример 4. Решить неравенство

Решение. Область определения неравенства: xÎ( – ¥; 3)È(3; + ¥).

Для применения метода возведения в квадрат необходимо ввести дополнительное ограничение на значения переменной x. Поэтому рассмотрим два случая.

1) x £ 0. Все отрицательные значения переменной являются решениями, так как в этом случае левая часть неравенства положительна, а правая – отрицательна; x = 0 – так же решение, в чем убеждаемся непосредственной подстановкой этого значения.

2) x > 0, x ¹ 3. Обе части неравенства положительны. Возводим их в квадрат, переходя к равносильному неравенству:

Ответ. xÎ( – ¥; 1]È[5; + ¥).

Пример 5. Решить уравнение

Решение. Область определения уравнения: xÎR. Так как обе части уравнения положительны, возводя их в квадрат, придем к равносильному уравнению

Ответ.

Пример 6. Решить неравенство

Решение. Область определения неравенства задается условиями x > 0, x ¹ 1, x ¹ 2. Или в другой форме: xÎ( 0; 1)È(1; 2)È(2; + ¥).  Избежать отдельного рассмотрения трех интервалов позволит умножение обеих частей на 2 и затем возведение модуля в квадрат.

Воспользуемся теперь монотонностью логарифмической функции: возрастанием при x >1 и убыванием при 0< x <1.

Таким образом, решениями являются все значения переменной из области определения.

Ответ. xÎ( 0; 1)È(1; 2)È(2; + ¥).