Функции
вида y=sinx, y=cosx, y=tgx, y=ctgx называются основными тригонометрическими функциями числового
аргумента x.
Функция
y=sinx и
некоторые ее свойства
1. Область определения D(sinx) = R.
2. Область значений E(sinx)=[–1;1].
3. Функция периодическая с наименьшим положительным периодом T=2p.
4. Нули
функции x = pn, nÎZ.
5. Функция нечетная,
sin(–x)= –sinx.
График симметричен относительно начала координат.
6. Интервалы монотонности: y=sinx
возрастает на промежутках [–p/2+2pn; p/2+2pn],
убывает на промежутках [p/2+2pn; 3p/2+2pn], nÎZ.
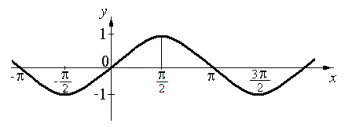
График
функции y=sinx
Функция
y=cosx и
некоторые ее свойства
1. Область определения D(cosx)=R.
2. Область значений E(cosx)=[–1;1].
3. Функция периодическая с наименьшим положительным периодом T=2p.
4. Нули функции p/2+pn, nÎZ.
5. Функция четная,
cos(–x)=cosx.
График симметричен относительно оси Oy.
6. Интервалы монотонности: y=cosx
возрастает на промежутках [–p+2pn; 2pn],
убывает на промежутках [2pn; p+2pn], nÎZ.
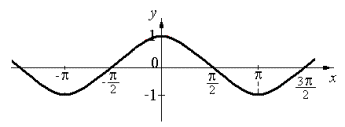
График
функции y=cosx
Функция
y=tgx и
некоторые ее свойства
1. Область определения D(tgx)=(–p/2+pn; p/2+pn), nÎZ.
2. Область значений
E(tgx)=R.
3. Функция периодическая с наименьшим положительным
периодом T=p.
4. Нули функции pn, nÎZ.
5. Функция нечетная,
tg(–x)= – tgx.
График симметричен относительно начала координат.
6. y=tgx монотонно возрастает на интервалах (–p/2+pn; p/2+pn), nÎZ.
.
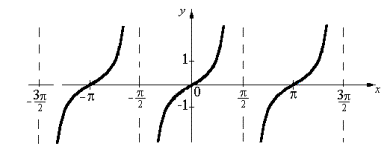
График
функции y=tgx
Функция
y=ctgx и
некоторые ее свойства
1. Область определения D(ctgx)=(pn; p+pn), nÎZ.
2. Область значений
E(ctgx)=R.
3. Функция периодическая с наименьшим положительным периодом T=p.
4. Нули функции p/2+pn, nÎZ.
5. Функция нечетная,
ctg(–x) = –ctgx. График
симметричен относительно начала координат.
6. y=ctgx монотонно убывает на интервалах (pn; p+pn), nÎZ.
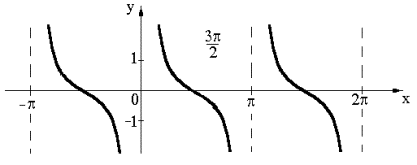
График
функции y=ctgx