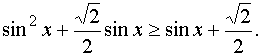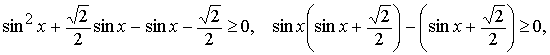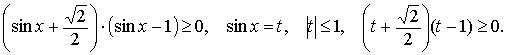Приведите неравенство к виду F(x)>0 (<,³,£). Если это возможно, разложите функцию F(x) на множители с помощью группировки, вынесения общего множителя за скобки или с помощью формул сокращённого умножения. Примените метод интервалов или используйте условие, при котором произведение множителей положительно, отрицательно, равно нулю.

Пример 1. Решить неравенство

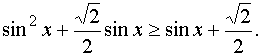
Решение. Область определения xÎR.

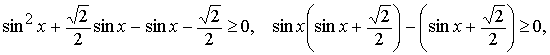
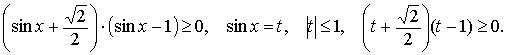
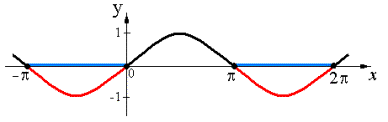
Используем метод интервалов:

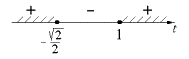
Из рисунка видно, что

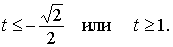
Учитывая, что | t |£1, получим

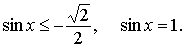
Решениями неравенства будут xÎ[-3p/4+2pn; -p/4+2pn], а решениями уравнения x = p/2+2pn.

Ответ. [-3p/4+2pn; -p/4+2pn] È {p/2+2pn}, nÎZ.

Пример 2. Решите неравенство

sinx(1+cosx)£1+cosx+cos²x.

Решение. Область определения xÎR.

sinx(1+cosx)–(1+cosx)£cos²x, (1+cosx)( sinx-1)£cos²x.

Применяя формулу sin²x+cos²x = 1, получим:

(1+cosx)( sinx-1)£1-sin²x, (1+cosx)( sinx-1)+sin²x-1£0.

Разложим левую часть неравенства на множители, применяя формулу

a²–b²=(a–b)(a+b) и вынесение общего множителя за скобки, получим:

(1+cosx)(sinx-1)+(sinx-1)(sinx+1)£0, (sinx-1)(1+cosx+1+sinx)£0.

Так как |sinx| £ 1 и |cosx|£1, то (1+cosx+1+sinx) ³ 0 при xÎR.

Значит, произведение двух множителей £ 0, если первый множитель sinx£0.

Получим -p+2pn £ x £ 0+2pn.
Ответ. [-p+2pn; 2pn], nÎZ.