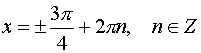2.1.2.Уравнения вида cosx=a, cosf(x)=a, |a|≤1

Теория и примеры

Решить уравнение cosx=a - значит найти множество всех углов (чисел) x, косинус которых равен a.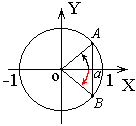

Построим единичную окружность и проведем прямую x=a, которая пересечёт окружность в точках А и В. Соединим эти точки с началом координат, получим углы x₁ с конечной стороной ОА и x₂ с конечной стороной ОВ, косинус которых равен a. Запишем их, учитывая периодичность функции y=cosx.

x₁= arccosa+2pm; x₂= – arccosa+2pm, mÎZ.

Объединим две формулы в одну x=± arccosa+2pn, nÎZ.

Уравнение вида cosf(x)=a, |a|≤1 решается с помощью выведенной формулы.

f(x)=± arccosa+2pn, nÎZ.

Пример 1. Решить уравнение.

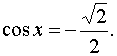
Решение. Область определения уравнения xÎR.

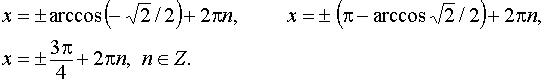
Ответ.

Пример 2. Решите уравнение

3cos(x/2) = 1.

Решение. Область определения уравнения xÎR.

cos(x/2)=1/3, x/2 = ± arccos(1/3)+2pn, x=±2arccos(1/3)+4pn, nÎZ.

Ответ. x = ± 2arccos(1/3) + 4pn, nÎZ.