2.1.3.Уравнения вида tgx=a, tg(f(x))=a, aÎR.

Теория и примеры

Решить уравнение tgx = a - значит найти множество всех углов (чисел) x, тангенс которых равен a.

На оси тангенсов найдем точку с ординатой, равной a. Проведем прямую через эту точку и начало координат, которая пересечёт единичную окружность в точках А и В. Получим углы x с конечными сторонами ОА и ОВ, тангенс которых равен a. Запишем их, учитывая периодичность функции y=tgx.

x=arctga+pn, nÎZ.

Уравнение вида tg(f(x))=a, aÎR, f(x)¹p/2+pn решается с помощью выведенной формулы

f(x)=arctga+pn, nÎZ.

 

Пример 1. Решить уравнение

                     

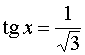
Решение. Область определения уравнения  xÎR, кроме x=p/2+pn.

   

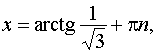
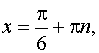
Ответ. x=p/6+pn, nÎZ.

Пример 2. Решить уравнение

                                    

Решение. Область определения уравнения xÎR, кроме x = 11^°+36^°n, т.к.

 5x+35^o¹90^o+180^on.

 x¹11^o+36^on.

      

Ответ. x = –19^°+36^°n, nÎZ.