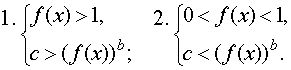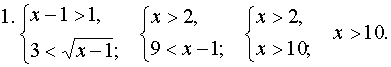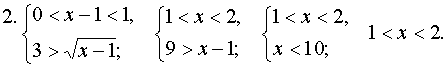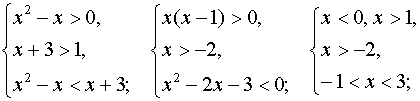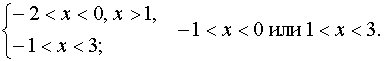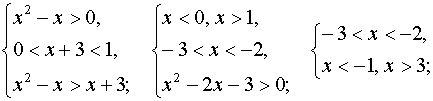2.1.3. Неравенства вида log_f(x) c > b, c > 0.

Как в пункте 2.1.1., представим число с в виде логарифма по основанию f(x),

b = log_f(x) (f(x)) ^b.

Неравенство примет вид log_f(x) c > log_f(x) (f(x)) ^b. Возможны два случая:

В ответ нужно записать объединение решений систем.

Нужно учитывать также область определения функции f(x).

Пример 1. Решить неравенство

log_x–13 < 1/2.

Решение. Представим число 1/2 в виде логарифма с основанием х – 1, 1/2 = log_x–1 (x – 1) ^1/2. Неравенство примет вид

log_x–1 3 < log_x–1 (x – 1) ^1/2.

Учитывая область определения и монотонность логарифмической функции, получим две системы неравенств

Ответ. 1 < x < 2; x > 10.

Пример 2. Решить неравенство

log_x+3 (x ² – x) < 1.

Решение. Запишем неравенство в виде

log_x+3 (x ² – x) < log_x+3 (x + 3)

Случай 1. Пусть х + 3 > 0, тогда функция log_x+3 t возрастает. Данное неравенство равносильно системе

Случай 2. Пусть 0 < x + 3 < 1, тогда функция log_x+3 t убывает. Данное неравенство равносильно системе

–3 < x < –2.

Объединим множества решений неравенства, полученных в случаях 1 и 2: –1 < x < 0; 1 < x < 3; –3 < x < –2.

Ответ. –3 < x < –2; –1 < x < 0; 1 < x < 3.